How resource-restricted devices can verify RLN proofs fast and efficiently.
Introduction
Recommended previous reading: Strengthening Anonymous DoS Prevention with Rate Limiting Nullifiers in Waku.
This post expands upon ideas described in the previous post, focusing on how resource-restricted devices can verify RLN proofs fast and efficiently.
Previously, it was required to fetch all the memberships from the smart contract, construct the merkle tree locally, and derive the merkle root, which is subsequently used to verify RLN proofs.
This process is not feasible for resource-restricted devices since it involves a lot of RPC calls, computation and fault tolerance. One cannot expect a mobile phone to fetch all the memberships from the smart contract and construct the merkle tree locally.
Constraints and requirements
An alternative solution to the one proposed in this post is to construct the merkle tree on-chain, and have the root accessible with a single RPC call. However, this approach increases gas costs for inserting new memberships and may not be feasible until it is optimized further with batching mechanisms, etc.
The other methods have been explored in more depth here.
Following are the requirements and constraints for the solution proposed in this post:
- Cheap membership insertions.
- As few RPC calls as possible to reduce startup time.
- Merkle root of the tree is available on-chain.
- No centralized services to sequence membership insertions.
- Map inserted commitments to the block in which they were inserted.
Metrics on sync time for a tree with 2,653 leaves
The following metrics are based on the current implementation of RLN in the Waku gen0 network.
Test bench
- Hardware: Macbook Air M2, 16GB RAM
- Network: 120 Megabits/sec
- Nwaku commit: e61e4ff
- RLN membership set contract: 0xF471d71E9b1455bBF4b85d475afb9BB0954A29c4
- Deployed block number: 4,230,716
- RLN Membership set depth: 20
- Hash function: PoseidonT3 (which is a gas guzzler)
- Max size of the membership set: 2^20 = 1,048,576 leaves
Metrics
- Time to sync the whole tree: 4 minutes
- RPC calls: 702
- Number of leaves: 2,653
One can argue that the time to sync the tree at the current state is not that bad. However, the number of RPC calls is a concern, which scales linearly with the number of blocks since the contract was deployed This is because the implementation fetches all events from the contract, chunking 2,000 blocks at a time. This is done to avoid hitting the block limit of 10,000 events per call, which is a limitation of popular RPC providers.
Proposed solution
From a theoretical perspective, one could construct the merkle tree on-chain, in a view call, in-memory. However, this is not feasible due to the gas costs associated with it.
To compute the root of a Merkle tree with leaves it costs approximately 2 billion gas. With Infura and Alchemy capping the gas limit to 350M and 550M gas respectively, it is not possible to compute the root of the tree in a single call.
Acknowledging that Polygon Miden and Penumbra both make use of a tiered commitment tree, we propose a similar approach for RLN.
A tiered commitment tree is a tree which is sharded into multiple smaller subtrees, each of which is a tree in itself. This allows scaling in terms of the number of leaves, as well as reducing state bloat by just storing the root of a subtree when it is full instead of all its leaves.
Here, the question arises: What is the maximum number of leaves in a subtree with which the root can be computed in a single call?
It costs approximately 217M gas to compute the root of a Merkle tree with leaves.
This is a feasible number for a single call, and hence we propose a tiered commitment tree with a maximum of leaves in a subtree and the number of subtrees is . Therefore, the maximum number of leaves in the tree is (the same as the current implementation).
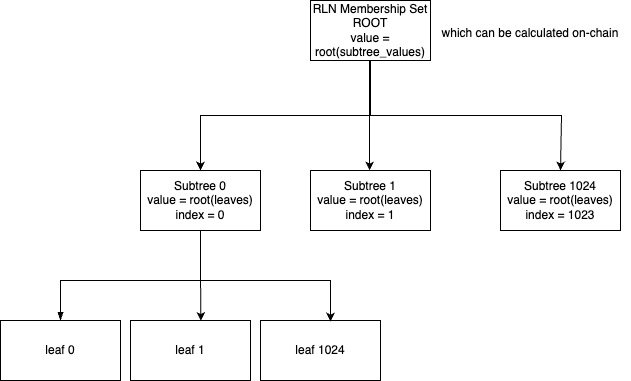
Insertion
When a commitment is inserted into the tree it is first inserted into the first subtree. When the first subtree is full the next insertions go into the second subtree and so on.
Syncing
When syncing the tree, one only needs to fetch the roots of the subtrees. The root of the full tree can be computed in-memory or on-chain.
This allows us to derive the following relation:
This is a significant improvement over the current implementation, which requires fetching all the memberships from the smart contract.
Gas costs
The gas costs for inserting a commitment into the tree are the same as the current implementation except it consists of an extra SSTORE operation to store the shardIndex of the commitment.
Events
The events emitted by the contract are the same as the current implementation,
appending the shardIndex of the commitment.
Proof of concept
A proof of concept implementation of the tiered commitment tree is available here, and is deployed on Sepolia at 0xE7987c70B54Ff32f0D5CBbAA8c8Fc1cAf632b9A5.
It is compatible with the current implementation of the RLN verifier.
Future work
- Optimize the gas costs of the tiered commitment tree.
- Explore using different number of leaves under a given node in the tree (currently set to 2).
Conclusion
The tiered commitment tree is a promising approach to reduce the number of RPC calls required to sync the tree and reduce the gas costs associated with computing the root of the tree. Consequently, it allows for a more scalable and efficient RLN verifier.